







Materialien für den Mathematikunterricht in den Klassen 8 bis 10
Bei Anmerkungen oder Fragen wenden Sie sich bitte per eMail an RalphSchwoerer@hotmail.com.
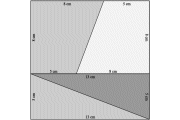
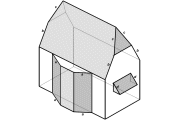
Wenn Sie das Programm Schaubilder vor dem 15. März 2007 herunter geladen und installiert haben, können Sie die für die Arbeitsblätter benötigten Aufgabendateien hier herunter laden.

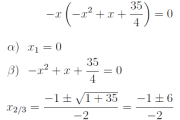
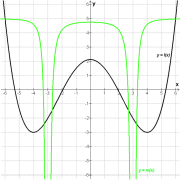
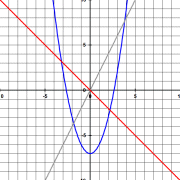
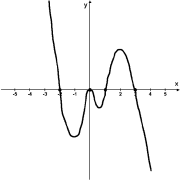
Wenn Sie diese kostenlose Materialsammlung unterstützen möchten, besuchen Sie meinen
![]() Partner-Shop.
Partner-Shop.